Resolva os quebra-cabeças de Kakuro

Neste guia, oferecemos uma série de dicas práticas sobre como resolver os quebra-cabeças de Kakuro, com dificuldades que vão do nível iniciante ao avançado.

Resumindo as regras: Kakuro é um jogo de quebra-cabeça em um tabuleiro semelhante a palavras cruzadas, onde dígitos são usados para fazer com que eles se somem aos valores especificados nos quadrados de definição do tabuleiro. Além disso, dentro de cada grupo de soma, cada dígito pode aparecer no máximo uma vez.

A maneira tradicional de resolver um quebra-cabeça de Kakuro é incremental: usando as informações existentes no quadro, você pode encontrar com certeza o valor de uma célula específica que pode assumir apenas um valor possível. Em seguida, esse valor é preenchido e o processo é repetido até que todas as células do quadro sejam descobertas.

Em algumas situações, não há uma célula de diretoria específica com apenas uma possibilidade. Nesses casos, cada uma das possibilidades precisa ser explorada sozinha e eliminada por meio de contradições até que reste apenas um curso de ação.

Apresentamos abaixo vários métodos para progredir na solução do quebra-cabeça real.

Somas exclusivos para definições específicas

Existem algumas definições que só podem ser resolvidas de uma forma específica:

• a soma 3 (em duas células) sempre será 1 + 2.
• a soma 4 (em duas células) sempre será 1 + 3.
• a soma 17 (em duas células) sempre será 8 + 9.
• a soma 6 (em três células) sempre será 1 + 2 + 3.
• a soma 24 (em três células) sempre será 7 + 8 + 9.

e assim por diante... Normalmente, você pode passar o mouse em uma grade de Kakuro sobre o número da definição e uma dica de ferramenta aparecerá contendo todas as possibilidades de escrever essa soma com dígitos exclusivos no número de células disponíveis.

As somas que podem ser escritas de uma maneira única geralmente são somas baixas ou altas, que forçam dígitos baixos/altos na resposta para obtê-las.

Ter uma maneira única de escrever a soma ajuda, mas lembre-se de que todas as permutações são válidas e você ainda precisa descobrir qual permutação real usar no quadro.

Restrições de linha/coluna

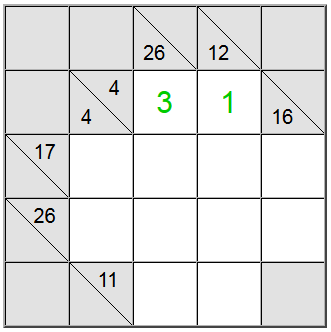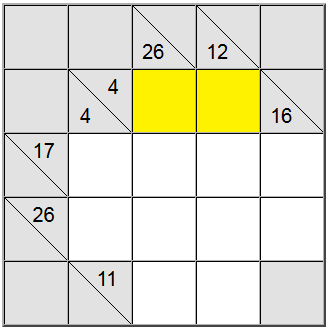
Para as células amarelas destacadas acima, há apenas uma maneira de escrever a soma: 4 = 1 + 3. No entanto, ainda precisamos descobrir qual permutação (1 + 3 ou 3 + 1) usar.

Acontece que a definição vertical de 26 nos ajuda: uma soma em 4 células que conteria o dígito 1 seria no máximo 1 + 9 + 8 + 7 = 25. Como nossa soma é 26, acontece que o dígito 1 não pode fazer parte da soma. Portanto, a única ordem restante para os quadrados amarelos é 3 + 1.

Definições, interseções

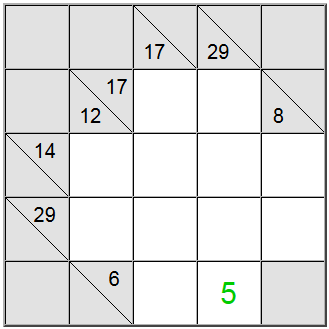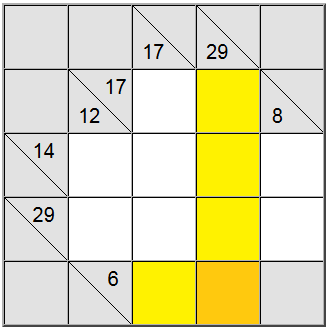
No quadro acima, os quadrados horizontais amarelos podem ser escritos como 6 = 1 + 5 ou 6 = 2 + 4. A soma vertical amarela só pode ser escrita como 29 = 5 + 7 + 8 + 9.

O quadrado amarelo encontrado na interseção dessas duas definições de soma deve conter o mesmo dígito, portanto, deve haver um dígito comum presente nas definições horizontal e vertical para ser compartilhado entre elas. Ao analisar as possibilidades acima, podemos facilmente descobrir que 5 é o único dígito que respeita esse critério.

Essa técnica funciona especialmente bem ao cruzar uma definição de soma baixa com uma de soma alta. As definições de soma baixa e alta são aquelas que têm um número de definição de soma relativamente baixa ou alta (6 e 29, respectivamente, para nosso exemplo) quando comparadas ao número de células disponíveis. Como 6 é relativamente baixo, ele forçará dígitos baixos na representação da soma e 29 forçará dígitos altos (para obter essas somas usando um determinado número de células). Portanto, é provável que a interseção de dígitos baixos e altos contenha apenas um candidato para o valor real da célula.

Valores mínimos/máximos para um grupo de soma

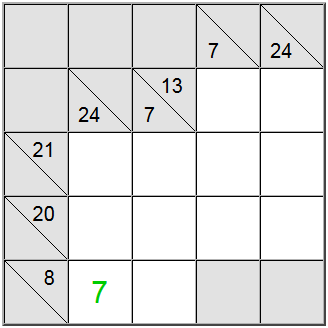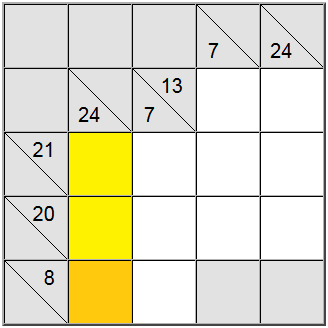
Às vezes, é útil descobrir o valor máximo ou mínimo de um grupo de soma. Isso pode dar uma ideia de qual é o intervalo válido de dígitos para essa soma específica, o que, por sua vez, o ajudará a fazer a correlação com outras restrições e descobrir as atribuições exclusivas no quadro.

No exemplo acima, as células verticais amarelas aceitam somente valores iguais a 7 ou superiores. Se você tentar atribuir um 6, poderá facilmente descobrir que 6 + 9 + 8 = 23, portanto, a soma da definição de 24 não seria alcançável.

Como 7 é o mínimo, a definição horizontal com 8 como soma força o 7 nessa posição.

Conclusão

Praticar é a melhor maneira de ver como esse conselho pode ser aplicado em jogos reais de Kakuro. Jogue um quebra-cabeça de verdade. Desejamos-lhe boa sorte e muita diversão!

Jogue Kakuro